Navigation : EXPO21XX > VISION 21XX > H15: Research and Universities > Royal Holloway, University of London
Royal Holloway, University of London
  • Offer Profile
  • MR is a set of tools that implements multiscale methods for processing 1D signals, 2D images, and 3D data volumes.

    What MR multiresolution analysis software offers
    • Scale and Resolution
    • Image and Data Analysis
    • Extensive Signal and Noise Modeling
    • Innovation and Performance
    • Financial Modelling, Nowcasting, Prediction
    • Wavelet and multiresolution transforms, ridgelet and curvelet transforms
Product Portfolio

  • Description

  • MR is a set of software components developed by CEA (Saclay, France) and Nice Observatory. This project originated in astronomy, and involved the development of a range of innovative methods built around multiscale analysis. The MR software components include almost all applications presented in the book Image and Data Analysis: the Multiscale Approach . Descriptions of these applications can also be found in many published papers. The goal of MR is not to replace existing image processing packages, but to complement them, offering the user a complete set of multiresolution tools. These tools are executable programs, which work on a wide range of platforms, independently of current image processing systems. They allow the user to perform various tasks using multiresolution, such as wavelet transforms, filtering, deconvolution, and so on. Programs can also be called from a Java interface. A set of IDL (Interactive Data Language, by Research Systems Inc.) and PV-Wave (Visual Numerics Inc.) routines are included in the package which interface the executables to these image processing packages. MR is an important package, introducing front-line methods to scientists in the physical, space and medical domains among other fields; to engineers in such disciplines as geology and electrical engineering; and to financial engineers and those in other fields requiring control and analysis of large quantities of noisy data.

    Wavelets and other multiresolution techniques have been developed in recent years, and furnish a powerful and insightful representation of the data. By means of multiresolution or multiscale analysis, an image can be decomposed into a set of images (or scales), each scale containing only structures of a given size. This data representation, associated with noise modeling, has been applied to very different applications such as data filtering, deconvolution, compression, object detection, and so on. Results are enhanced in all such processing because the wavelet transform approach allows a better understanding of how the data values are distributed in an image, and how the signal can be separated from the noise. The goal of this project is develop new methods for data processing using the multiscale approch. Several products, MR/1 , MR/2 , MR/3 ,and MR/4 have been realized.

  • MR/1: Multiresolution and Applications

  • MR/1 is a set of software components developed by CEA (Saclay, France) and Nice Observatory. This project originated in astronomy, and involved the development of a range of innovative methods built around multiscale analysis. The MR/1 software components include almost all applications presented in the book Image and Data Analysis: the Multiscale Approach . Descriptions of these applications can also be found in many published papers . The goal of MR/1 is not to replace existing image processing packages, but to complement them, offering the user a complete set of multiresolution tools. These tools are executable programs, which work on a wide range of platforms, independently of current image processing systems. They allow the user to perform various tasks using multiresolution, such as wavelet transforms, filtering, deconvolution, and so on. Programs can also be called from a JAVA interface. A set of IDL (Interactive Data Language, by Research Systems Inc.) and PV-Wave (Visual Numerics Inc.) routines are included in the package which interface the executables to these image processing packages. MR/1 is an important package, introducing front-line methods to scientists in the physical, space and medical domains among other fields; to engineers in such disciplines as geology and electrical engineering; and to financial engineers and those in other fields requiring control and analysis of large quantities of noisy data.

    Wavelet and Multiscale Transform
    Many 1D and 2D wavelet transforms and other multiscale methods, such the Pyramidal Median Transform or the lifting scheme, have been inplemented in MR/1 .

  • Noise Modeling:

    • Our noise modeling in the wavelet space is based on the assumption that the noise in the data follows a distribution law, which can be:
    • a Gaussian distribution
    • a Poisson distribution
    • a Poisson + Gaussian distribution (noise in CCD detectors)
    • Poisson noise with few events (galaxy counts, X-ray images, point patterns)
    • Speckle noise
    • Correlated noise
    • Root Mean Square map: we have a noise standard deviation of each data value.
       
    If the noise does not follow any of these distributions, we can derive a noise model from any of the following assumptions
    • it is stationary, and we have a subimage containing a realization of the noise,
    • it is additive, and non-stationary,
    • it is multiplicative and stationary,
    • it is multiplicative, but non-stationary,
    • it is undefined but stationary,
    • it is additive, stationary, and correlated.

  • Applications:

  • 1.    Descriptions of these applications can also be found in many published papers .
    2.    General tools: data conversion, simulation, statistic, Fourier analysis, mathematical morphology, principal component analysis, ...
    3.    1D and 2D wavelet transform and reconstruction..Multiscale object manipulation: statistic, band extraction, comparison, ...
    4.    Multiresolution support detection.
    5.   1D and 2D filtering taking into account the different noise models. Many methods have been implemented (11 in 1D and 18 in 2D) including standards like K
           Sigma  thresholding, SURE, MAD, Universal thresholding, Multiscale Wiener filtering, ...
    6.    Image background subtraction.
    7.    Image deconvolution: nine standard deconvolution methods are available (MEM, LUCY, Landweber, MAP, ...), and five wavelet based methods.
    8.    Image registration.
    9.    Lossy and lossless image compression. the PMT (median based compression method) and the bi-orthogonal wavelet transform allows both the user to
           reconstruct an image (or a part of an image) at a given resolution. Lossless image compression is based on the lifting scheme.
    10.  Object detection and extraction in 1D and 2D data set using the Multiscale Vision Model.
    11.  Edge detection and image reconstruction from the multiscale edges. Many standard edge detection methods are available (15) and two wavelet based methods.
    12.  Contrast enhancement. Standard methods and contrast enhancement methods based on the wavelet transform are available.
    13. 1D Wavelet Transform Modulus Maxima (WTMM) representation and reconstruction.
    14. 1D Multifractal analysis.
    15. Time-Frequency analysis (Short Term Fourier Transform, Wigner-Ville transform).
    16. Time series nowcasting and forecasting.

  • MR/2: Multiscale Entropy and Applications

  • The term "entropy" is due to Clausius (1865), and the concept of entropy was introduced by Boltzmann into statistical mechanics, in order to measure the number of microscopic ways that a given macroscopic state can be realized. Shannon (1948) founded the mathematical theory of communication when he suggested that the information gained in a measurement depends on the number of possible outcomes out of which one is realized. Shannon also suggested that the entropy can be used for maximization of the bits transferred under a quality constraint. Jaynes (1957) proposed to use the entropy measure for radio interferometric image deconvolution, in order to select between a set of possible solutions that which contains the minimum of information, or following his entropy definition, that which has maximum entropy. In principle, the solution verifying such a condition should be the most reliable. Much work has been carried out in the last 30 years on the use of entropy for the general problem of data filtering and deconvolution. Traditionally information and entropy are determined from events and the probability of their occurrence. Signal and noise are basic building-blocks of signal and data analysis in the physical and communication sciences. Instead of the probability of an event, we are led to consider the probabilities of our data being either signal or noise. Consider any data signal with interpretative value. Now consider a uniform "scrambling" of the same data signal. (Starck et al., 1998, illustrate this with the widely-used Lena test image.) Any traditional definition of entropy, the main idea of which is to establish a relation between the received information and the probability of the observed event, would give the same entropy for these two cases. A good definition of entropy should instead satisfy the following criteria:
    • 1.The information in a flat signal is zero.
    • 2.The amount of information in a signal is independent of the background.
    • 3.The amount of information is dependent on the noise. A given signal Y (Y = X + Noise) doesn't furnish the same information if the noise is high or small.
    • 4.The entropy must work in the same way for a signal value which has a value B + epsilon (B being the background), and for a signal value which has a value B - epsilon.
    • 5.The amount of information is dependent on the correlation in the signal. If a signal S presents large features above the noise, it contains a lot of information. By generating a new set of data from S, by randomly taking the values in S, the large features will evidently disappear, and this new signal will contain less information. But the data values will be the same as in S.
    To cater for background, we introduce the concept of multiresolution into our entropy. We will consider that the information contained in some dataset is the sum of the information at different resolution levels, j. A wavelet transform is one choice for such a multiscale decomposition of our data. We define the information of a wavelet coefficient wj(k) at position k and at scale j as I = - ln (p(wj(k))), where p is the probability of the wavelet coefficient. Entropy, commonly denoted as H, is then defined as the sum over all positions, k, and over all scales, j, of all I. For Gaussian noise we continue in this direction, using Gaussian probability distributions, and find that the entropy, H, is the sum over all positions, k, and over all scales, j, of (wj(k)^2)/(2 sigma^2 j) (i.e. the coefficient squared, divided by twice the standard deviation squared of a given scale). Sigma, or the standard deviation, is the (Gaussian) measure of the noise. We see that the information is proportional to the energy of the wavelet coefficients. The higher a wavelet coefficient, then the lower will be the probability, and the higher will be the information furnished by this wavelet coefficient. Our entropy definition is completely dependent on the noise modeling. If we consider a signal S, and we assume that the noise is Gaussian, with a standard deviation equal to sigma, we won't measure the same information compared to the case when we consider that the noise has another standard deviation value, or if the noise follows another distribution. Returning to our example of a signal of substantive value, and a scrambled version of this, we can plot an information versus scale curve (e.g. log(entropy) at each scale using the above definition, versus the multiresolution scale). For the scrambled signal, the curve is flat. For the original signal, it increases with scale. We can use such an entropy versus scale plot to investigate differences between encrypted and unencrypted signals, to study typical versus atypical cases, and to differentiate between atypical or interesting signals.

  • MR/3: 3D and Multichannel Data

  • MR/3 deals with the analysis of multi-channel data or 3D data.
    3D data can either be a real cube, or a set of images of the same observation, but taken at different times. Multi-channel data can be either 1D or 2D multi-channel:
    • 1D multi-channel: a 1D signal is observed at several wavelength or at different times. The result is an image.
    • 2D multi-channel: a 2D signal (image) is observed at several wavelengths or at different times. The result is a cube. A special case of multi-channel images is color images. In this case, we have three channels. Several color coordinate systems exist. The most widely-used is the RGB system. Each pixel is identified by three values R, G, and B corresponding to the three colors red, green, and blue. Applications in MR/3 are

      1. General tools: statistic, operations, noise simulation, conversion ....
      2. Cube and Wavelet transform

        1. 3D a trous wavelet transform and reconstruction.
        2. 3D bi-orthogonal wavelet transform and reconstruction.
        3. 3D Wavelet transform manipulation (band extraction, ...).
        4. 3D data filtering using the wavelet transform.
      3. Multi-channel Data
        1. 1D and 2D Wavelet Karhunen-Loeve transform (WT-KLT) and reconstruction.
        2, 1D and 2D multichannel data filtering using the WT-KLT.
        3. Independent Component Analysis.
      4.Color images
        1 .RGB image compression.
        2. RGB image filtering.
        3. RGB image contrast enhancement.
      5. Multi-temporal images
        1. Images coaddition taking into account vertical and horizontal shifts.
        2. Images deconvolution taking into account vertical and horizontal shifts.

  • MR/4: Ridgelet and Curvelet

  • MR/4 deals with the ridgelet and the curvelet transforms.
    Wavelets presents some limitations when the data present anisotropic features. New methods, such the ridgelet transform and the curvelet transform, are better adapted to this kind of data. Wavelets, Ridgelets and Curvelets can also be combined in order to benefit of the advantages of each of them.
    Applications in MR/4 are

    General tools: statistic, operations, noise simulation, conversion ....
    1. 2D Ridgelet:
      1. Ridgelet transform and reconstruction of images.
      2. Statistics relative to ridgelet coefficients.
      3 Image Ridgelet filtering.

    2. 2D Curvelet:

      1. Curvelet transform and reconstruction of images.
      2. Statistics relative to curvelets coefficients.
      3. Curvelet filtering.
      4. Contrast enhancement by the Curvelet transform.

    3. Color images and Curvelets:

      1. RGB image contrast enhancement by the Curvelet transform.
      2. RGB image Curvelet filtering.

    4. Combined Filtering Method.

  • Sparse Image and Signal processing

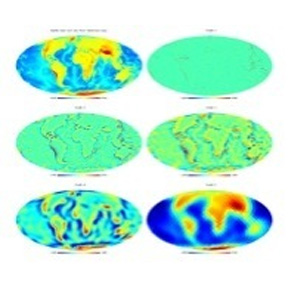
    • Pyramidal Wavelet Transform on the Sphere

    • The global relief data are ETOPO5 land and sea-floor elevation data. The isotropic pyramidal wavelet transform preserves detail, and is efficient in storage and computation. Chapter 10 discusses many aspects of multiscale geometric analysis on the sphere.

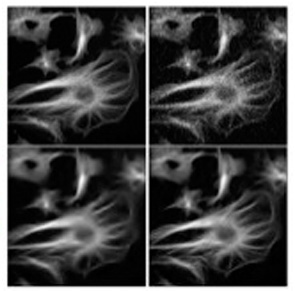
    • Filtering Biomedical Microscope Images
       

    • The image (upper left) is of fluorescent tubulin filaments. Upper right then is a noisy version, with Poisson noise. The lower images are filtered, as discussed in Chapter 6. This noise filtering is based on the curvelet transform for preservation of faint features.

    • Signal Recovery from Compressed Sampling

    • Compressed sensing simultaneously samples and compresses the signal. The image of Piet Mondrian's painting is an example used in Chapter 11 to show how compressed sensing handles acquisition and transmission of large amounts of image data.